At Shap we offer children a broad maths curriculum, following the objectives set out in the National Curriculum and Early Years Foundation Stage Statutory Framework. We deliver these through a mastery approach. A typical maths lesson provides the opportunity for all children, regardless of their ability, to develop and flourish into confident and capable mathematicians through the use of teaching for mastery strategies.

Our subject leader works closely with the North North West Maths Hub and is currently training to be a Primary Mastery Specialist. 

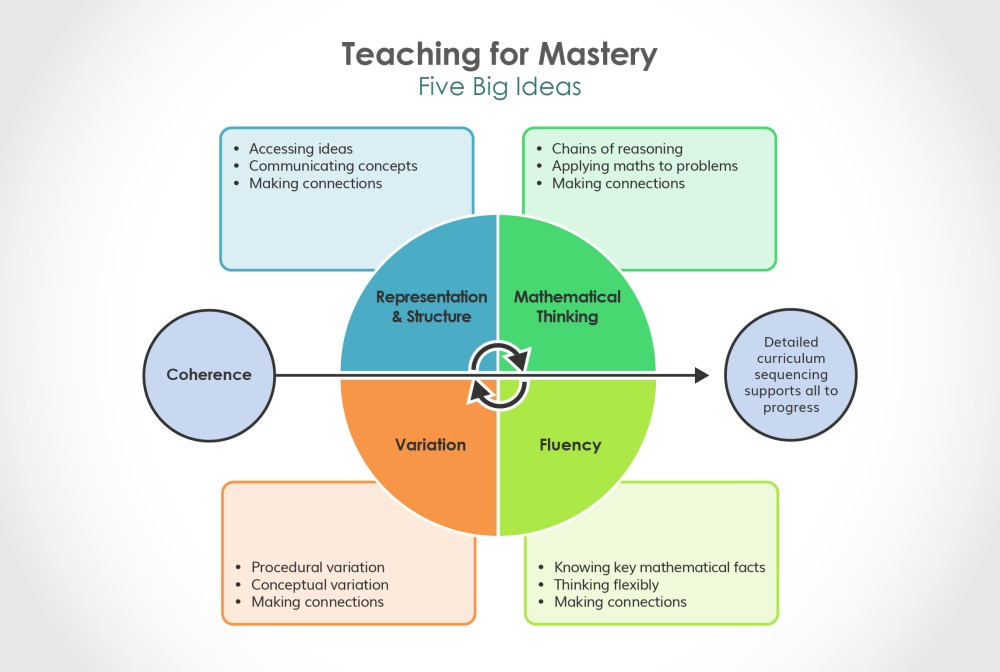
Teaching for mastery is underpinned by the Five Big Ideas (Debbie Morgan, NCETM). These have been informed by research evidence and classroom experience over many years and for the basis of our teaching and learning for maths at Shap. These ideas permeate all maths lessons and guide teacher's planning. 

Coherence

Lessons are broken down into small, connected steps that gradually unfold the concept and provides access for all children. These small steps will lead to a generalisation of the concept and the ability to apply the concept to a range of contexts.

At Shap, teachers use small steps from the White Rose Maths resources to plan a coherent series of lessons to break down large concepts into manageable and meaningful steps.

Fluency

Fluency comes from deep knowledge, repetition and practise. When children are fluent in a concept they are able to:

• rapidly recall key facts such as times tables and number bonds and procedures to calculate and solve questions;
• have greater accuracy when completing calculations with few or no careless errors;
• retention of knowledge and understanding on a separate occasion to when the concept was first introduced (for example, in a different week, month, term or year);
• have the flexibility to move between different contexts and representations of mathematics.

At Shap, fluency is a part of all lessons, either in the starter activity recapping prior learning and needs to be used in the main part of the lesson. We give children regular practice and repetition activities to develop fluency with a particular focus on number including: rapid recall of times tables, number bonds and mental calculations appropriate to each year group.

Fluency tasks will be given in lessons or as early morning work and can take the form of: chanting, mental arithmetic tests, Learn Its and CLICs taken from Big Maths, whole class or group games.

We have recently introduced Mastering Number EYFS and KS1 and have applied to be part of Mastering Number KS2. These are programmes designed by the NCETM to develop number sense and fluency skills. 

Representation and Structure

Representations used in lessons expose the mathematical structure being taught. The representation needs to pull out the concept being taught, and in particular, the key difficulties or misconceptions children might encounter.

There will be some key representations which the children will meet time and again.

At Shap, teachers will plan and use the concrete, pictorial, abstract approach across some, or all, of their lessons, allowing children to see the mathematical structure behind a concept. These are deliberately and carefully chosen.

Teachers have access to a range of concrete manipulatives as well as interactive visual, pictorial representations to use with children in lessons. Teachers will also use stem sentences, where appropriate, which describe the representation and helps the children move to working in the abstract.

Mathematical Thinking and Talking

If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others. Mathematical thinking can involve:

• looking for patterns in order to discern structure;
• looking for relationships and connecting ideas;
• reasoning logically, explaining, conjecturing and proving 

Mathematical thinking is expressed through talking. A maths classroom should never be quiet.

To encourage mathematical talking, teachers may use stem sentences to help children structure their talk. For example: The denominator is .... because the whole has divided into .... equal parts.

Teachers will also give children sentence scaffolds to enable them to express their ideas. Some examples are:

• It can’t be… because…
• I noticed that…
• This is true/false because…
• I already know that … so …
• This is always/never true because…
• This is the same/different because…

Children should be able to explain how they gained an answer and express why they believe it is the right answer. This mathematical talk is the foundation for reasoning skills and will build children’s confidence to communicate their ideas clearly and concisely before writing them down.

At Shap, teachers will scaffold and facilitate mathematical thinking through targeted and differentiated questioning. We ask children to explain, convince, draw diagrams to illustrate an idea or strategy. Teachers provide regular, purposeful opportunities for mathematical talk using a 'ping-pong' style approach.

Teachers model the correct use of mathematical vocabulary and expect children to use the correct age-appropriate vocabulary in lessons too. 

Variation

Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the episodes, activities and exercises used within a lesson and follow-up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure.

At Shap, variation is used in questions given to children in their practice of a concept, tackling the same concept or procedure through different types and structures of questions. Standard and non-standard examples are used to develop children's understanding of what something is or something is not and essential and non-essential features.